Pools
Capital is required for traders to get leverage on the platform. For this, there are Liquidity Pools(LPs): anyone can become a liquidity provider by depositing funds in the Liquidity Pool.
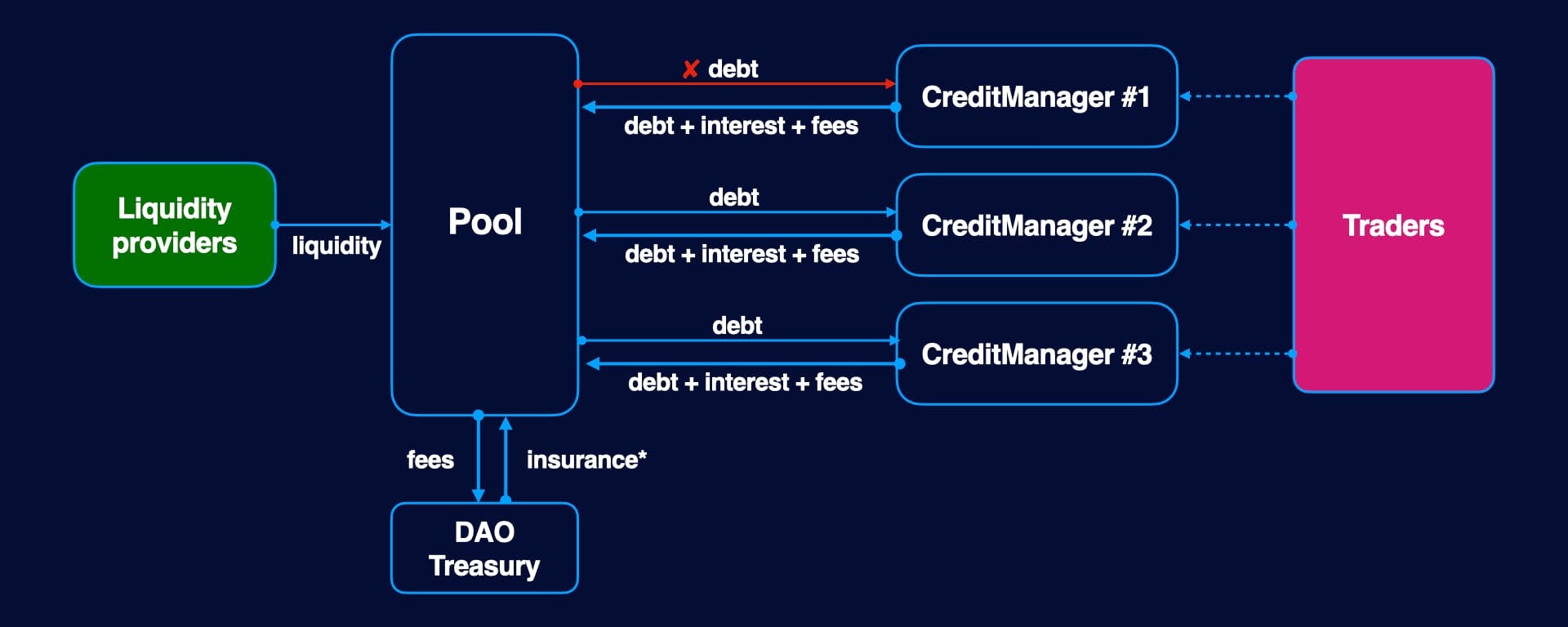
The profitability of LPs depends on the pool utilization ratio - the higher utilization, the higher interest rate. Each pool has an underlying asset and risk parameters such as: allowed trading tokens, allowed DEXes, stable coin pool, and others.
Currently pools use two points linear extrapolation for base interest rate calculation.
Basic parameters
- EL(t) - expected liquidity
- B(t) - total borrowed
- r(t) - borrow rate
- d(t) - diesel rate
- CI(t) - cumulative index (it shows value of money at moment t)
Periods and timestamp
All functions are piecewise linear functions. Each change in available liquidity or borrowed amount updates rate parameters. In follow formulas we use the convention:
Available liquidity
The amount of money available in pool.
EL(t) - Expected Liquidity
The amount of money should be in the pool if all users close their Credit Accounts and return debt. If no action happens during and , then the equation of should be
Beside, Add Liquidity and Remove Liquidity will have a new formula of .
B(t) - Total borrowed
Represents total borrowed amount without accrued interest rate:
r(t) - Borrow APY
Represents current borrow APY. Depends on pool utilisation parameter and computed independently using Interest rate model.
d(t) Diesel rate
Liquidity providers get profits from holding diesel tokens because they grow with expected interest. LP can keep diesel tokens on their wallets and then withdraw the deposit + interest.
Diesel Rate is the price of Diesel token (LP token).
Cumulative Index
Cumulative Index is aggregated variable that shows value of borrowing money.
Rate parameters update
Updates borrow rate & cumulative index. Called each time when borrowed amount or available liquidity is changed:
- Add liquidity
- Remove liquidity
- Credit account manager lends money
- Credit account manager repays debt